Berechne die Höhe eines Baumes mit Hilfe seines Schattens!

Durchführung

Diese Methode ist besonders geeignet für sehr hohe, freistehende Bäume, aber auch für Gebäude, Masten u.s.w. Sie funktioniert allerdings nur, wenn man auch den ganzen Schatten des zu messenden Objektes sehen kann. 

Zuerst misst man, falls unbekannt, seine eigene Körpergröße. Die Messung kann in Metern oder Zentimetern sein, es ist nur wichtig dass für alle Messungen die gleiche Einheit benutzt wird. 

Danach misst man die Länge des eigenen Schattens; dies klappt am Besten im Team zu zweit. Muss man alleine messen, kann man sich aber eines Tricks bedienen, damit das Ganze nicht zur Schattenjagd ausartet: Man stellt sich einfach so hin, dass der eigene Schatten an einer klar erkennbaren Stelle (z.B. Grund eines Baumstamms) endet und misst dann die Distanz vom eigenen Standpunkt zum vorher gemerkten Ende seines Schattens.

Schließlich misst man die Länge des Schattens des zu bestimmenden Objektes, z.B. ein Baum. Es ist wichtig, dass man den ganzen Schatten des Objektes sehen kann.

Die Höhe des Objekts kann nun mathematisch berechnet werden, denn bei gleichem Sonneneinfall ist das Verhältnis zwischen der Höhe des Vermessers und der Länge seines Schattens das gleiche als das Verhältnis zwischen der Höhe des Objektes und der Länge des Objektschattens.

Also:

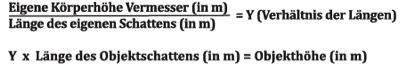
Doch Achtung: Der Wert Y gilt nur für eine kurze Zeit (ungefähr 20 Minuten); ändert sich der Stand der Sonne, ändert sich der Schatten und damit auch Y.

Eine ähnliche Methode benutzte der griechische Philosoph und Mathematiker Thales von Milet ca. 600 v. Chr , um die Höhe der Cheops-Pyramide in Gizeh, Ägypten zu messen.

Tipps

Am besten funktioniert dies an einem sonnigen, hellen Tag und auf ebenem Boden. Steht das zu messende Objekt (z.B. ein Baum) an einem Hang, ist es schwieriger möglichst genaue Messungen zu machen.

Alle Messungen müssen in der gleichen Einheit gemacht werden (Meter oder Zentimeter). 

Autor: Joseph Rodesch (FNR), Liza Glesener
Foto: FNR