
Luxembourg Science Center
Die Wissenschaftsvermittlerin Gina Reuland bei einer Statistik-Show im Luxembourg Science Center.
56%, 95%, oder waren es doch 99%? Die Wirksamkeit verschiedener Impfstoffe wird in den Medien oft durch einfache Prozentangaben miteinander verglichen und zusammengefasst. Doch was bedeuten diese Angaben genau? Wie präzise sind sie? Und was bedeutet es, wenn Forscher in ihren Studien ganze Intervalle angeben? Im folgenden Artikel gehen wir diesen Fragen auf den Grund und versuchen die dazugehörigen statistischen Konzepte zu entschlüsseln.
Um die statistischen Konzepte von Studien besser zu verstehen, simulieren wir eine Studie, die dem Klischee auf den Grund geht, dass Luxemburger Frauen multitaskfähiger sind als Männer. Eine Stichprobe von 100 Frauen und 100 Männern nimmt an der Studie teil. Die Teilnehmer sollen in einer bestimmten Zeit jeweils zwei Aufgaben gleichzeitig erledigen, sagen wir zum Beispiel eine Nachricht schreiben und einem Gespräch zuhören. Danach wird vom Forschungsteam kontrolliert ob diese Aufgaben adäquat gelöst wurden und die Anzahl erfolgreicher Frauen und Männer angeben.
Angenommen 60% der Frauen in der Stichprobe haben beide Aufgaben erfolgreich absolviert, so wäre eine Hochrechnung auf die Gesamtbevölkerung mit der Aussage „60% der Frauen in Luxemburg sind multitaskfähig“ dann doch statistisch gesehen etwas unseriös. Warum? Es könnte sein, dass die Stichprobe nicht gut ist, trotz aller Mühe sie bestmöglich zu wählen. Inwiefern können wir den Ergebnissen dieser Studie also vertrauen?
Eine gute Stichprobe, ein gutes Studiendesign und statistische Datenanalyse sind wichtig, damit die Ergebnisse vertrauenswürdig und aussagekräftig sind. .
Was ist eine gute Stichprobe?
Eine Stichprobe ist gut, wenn sie repräsentativ für die Bevölkerung ist, d.h. wenn sie die ganze Population in all ihren Merkmalen möglichst gut widerspiegelt. „In all ihren Merkmalen“ ist nicht gerade konkret, weshalb die Repräsentativität an sich auch kein wissenschaftlicher Ausdruck ist.
Was damit gemeint ist, ist aber weitaus anerkannt und klar: Die Stichprobe soll ein bestmögliches Abbild der Population darstellen. Die Forscher identifizieren die für ihre Studie relevanten Merkmale der Bevölkerung und ziehen aus jeder Bevölkerungsschicht mit dem identifizierten Merkmal zufällig Probanden. Diese Merkmale sollten jeweils, entsprechend ihrem wahren Anteil in der Bevölkerung, in der Stichprobe vertreten sein.
Solch eine sogenannte geschichtete Zufallsstichprobe wird idealerweise auch bei Studien zur Wirksamkeit von Impfstoffen oder Medikamenten gezogen, die für die gesamte Bevölkerung zugelassen werden sollen. Hauptmerkmale wären hier zum Beispiel Geschlecht, Alter, Body-Mass-Index und Herkunft.
In der Praxis ist das aber nicht immer der Fall. So werden zum Beispiel ältere Menschen bei klinischen Studien oft ausgeschlossen. Ein Grund: sie leiden oft an mehreren Krankheiten gleichzeitig, was es schwerer macht, die Wirksamkeit eines Medikaments und/oder die Ursache für eventuell auftretende Nebenwirkungen auszumachen.

Im Luxembourg Science Center kann man anhand einer Stichprobe (man ziehe 25 aus 1000) schätzen wie viele rote Kugeln sich in der großen Sphäre befinden. In der Stichprobe auf dem Foto sind 4 der 25 Kugeln rot (siehe Bildschirm im Hintergrund) was geschätzte 160 rote Kugeln im ganzen bedeuten würde.
Wie vertrauensvoll sind denn repräsentative Studien?
Auch wenn eine gute, repräsentative Stichprobe gewählt wurde gilt: Basiert sich ein Studienergebnis nur auf einer einzigen Stichprobe, dann wird dieses in den seltensten Fällen mit dem wahren gesuchten Wert der ganzen Bevölkerung exakt übereinstimmen. Denn dafür müsste die ganze Bevölkerung an der Studie teilnehmen. Es wird immer Abweichungen geben.
Aus diesem Grund sind die Intervalle, die oft von Forschern in Studien zusammen mit ihren Ergebnissen angegeben werden, wesentlich. Diese Intervalle, auch noch Konfidenz- oder Vertrauensintervalle genannt, geben einen Bereich an, der den wahren gesuchten Wert der Bevölkerung höchstwahrscheinlich enthält. Einfach gesagt könnte ein 95% Konfidenzintervall wie folgt beschrieben werden: Würden die Forscher die Studie 100-mal wiederholen, dann würden 95 von 100 angegebenen Intervallen den wahren Wert der Gesamtbevölkerung enthalten und 5 nicht. In 95 von 100 Fällen könnte man dem Studienergebnis also vertrauen.
Infobox
Auf der Basis ihrer Zufallsstichprobe bestimmen die Forscher einen Bereich, der den wahren gesuchten Wert der Bevölkerung höchstwahrscheinlich enthält. Dabei gehen sie folgendermaßen vor:
Im Vorfeld ihrer Studie legen die Forscher fest, wie wahrscheinlich es ist, dass sie sich irren und der wahre Wert nicht in dem berechneten Intervall liegt. Diese sogenannte Irrtumswahrscheinlichkeit, liegt oft bei 5%.
Warum 95% und nicht 100%? Je mehr man sich den 100% annähert, je grösser wird das Intervall und umso schwerer wird es, statistische signifikante Unterschiede zwischen zwei Gruppen zu erkennen – mehr dazu gleich. So hat sich eine 95%ige Sicherheit in vielen Forschungsgebieten als hilfreich erwiesen und durchgesetzt.
Was bedeutet das nun für die Aussagekraft unserer oben beschriebenen, fiktiven Studie? Die Forscher würden zwei Konfidenzintervalle berechnen, eins für Männer und eins für Frauen, die die jeweilige Position des wahren Wertes der Bevölkerung abschätzen. Überschneiden sich die Intervalle am Ende, so kann man statistisch keinen signifikanten Unterschied der Multitaskfähigkeit zwischen Männer und Frauen feststellen. Überschneiden sie sich jedoch nicht, so gibt es einen statistisch signifikanten Unterschied zwischen den Geschlechtern! Und diesem Ergebnis können wir dann vertrauen.
In der folgenden interaktiven Grafik kannst du das selbst simulieren. Verschiebe anhand der Slider den in der Stichprobe beobachteten Anteil multitaskfähiger Frauen (pF) und Männer (pM) und beobachte, wann sich die Konfidenzintervalle (gelbe und blaue Fläche unter den Kurven) überschneiden und wann nicht. Du kannst auch den Stichprobenumfang (n) von Männern respektiv Frauen ändern. So siehst Du z.B., dass bei einer Stichprobe von 100 Frauen bzw. Männern und einer Multitaskfähigkeit der Frauen von 60% (pF = 0,6) der Unterschied in der Multitaskfähigkeit der beiden Gruppen statistisch signifikant wäre, wenn er mindestens 20 Prozentpunkte beträgt, also pM ≤ 0,4 oder pM ≥ 0,8.
Was passiert, wenn sich der Stichprobenumfang vergrößert?
Die Konfidenzintervalle werden mit zunehmender Größe der Stichprobe schmaler und damit unsere Schätzung präziser und die Aussagekraft der Studie grösser! Wollen die Forscher das 95% Intervall halbieren, also die Genauigkeit der Studie sozusagen verdoppeln, dann müssen sie den Stichprobenumfang vervierfachen. Beim Bestimmen des Stichprobenumfangs, legen die Wissenschaftler also die Breite des Konfidenzintervalls und damit die Aussagekraft ihrer Studie fest.
Und was wäre, wenn die Forscher nicht die Multitaskfähigkeit der Luxemburger, sondern der Deutschen, Amerikanischen, Chinesischen oder der ganzen Weltbevölkerung testen wollen würden? Müsste der Stichprobenumfang dann proportional mit der Bevölkerungszahl wachsen?
Nicht unbedingt! Die Methode der geschichteten Zufallsprobe garantiert, dass die gezogene Stichprobe an sich eine kleine Bevölkerung genauso zuverlässig repräsentiert wie eine größere. Aber je grösser der Umfang der Stichprobe, um so schmaler fällt der Konfidenzintervall aus und umso präziser und aussagekräftiger ist die Studie.
Was bedeutet das denn nun im Fall der Covid-19-Impfstoffstudien?
Im Januar 2021 lagen in der EU die Notzulassungen für Covid-19-Impfstoffe der Unternehmen AstraZeneca, Moderna und BioNTech/Pfizer vor. Im März folgte die von Johnson & Johnson. Die Europäischen Ärzneimittelagentur EMA erteilte die Zulassungen des Impfstoffs Vaxzevria von AstraZeneca auf Basis der Zwischenergebnisse von klinischen Studien. Nehmen wir diese Ergebnisse unter die Lupe.
5807 Probanden erhielten den Impfstoff und 5829 Probanden ein Placebo. In der ersten Gruppe erkrankten 30 Personen an symptomatischem Covid-19, in der zweiten 101. Die Wirksamkeit eines Impfstoffs ist nun der Prozentanteil der Probanden, die dank des Impfstoffs vor einer Erkrankung verschont blieben. Was heißt das genau?
Da in der Impfstoffgruppe 101-30 = 71 weniger Probanden als in der Kontrollgruppe erkrankten, blieben genau diese im Durchschnitt vor einer Erkrankung verschont, was einer Wirksamkeit von ungefähr 70% in der veröffentlichten Studie entspricht. Das bedeutet, dass von 100 Geimpften, die mit dem Virus in Kontakt kommen, im Durchschnitt etwa 70 vor einer Erkrankung geschützt sind. In anderen Worten: Wäre die gesamte Luxemburger Bevölkerung vor der Pandemie mit AstraZeneca geimpft worden, hätte es, nach aktuellem Stand (Anfang Juni 2021), vermutlich keine 70.000 sondern nur ungefähr 21.000 Infizierte gegeben.
Natürlich brauchen wir jetzt ein Konfidenzintervall, um abzuschätzen, inwieweit wir dieser Wirksamkeit von 70,4% aus den klinischen Studien trauen können. Ein wichtiger Faktor zur Bestimmung der Breite des Intervalls ist das Verhältnis zwischen dem Anteil der Covid 19 Erkrankten in der Impfstoff- und jenem in der Kontrollgruppe, das sogenannte relative Risiko.
In der Studie von AstraZeneca erkrankten 30 von 5807 der Probanden in der Impfstoffgruppe, was 0,52% entspricht. In der Kontrollgruppe waren es 1,73%. Damit erhalten wir ein relatives Risiko von 0,52 / 1,73 = 0,3. Je weniger Erkrankte wir in der Impfstoffgruppe und je mehr Erkrankte wir in der Kontrollgruppe haben, je kleiner wird dieses Verhältnis. Ein kleineres relatives Risiko erhöht unser Vertrauen in die Wirksamkeit des Impfstoffs und führt somit zu einem kleineren und präziseren Konfidenzintervall und also zu einer aussagekräftigeren Studie.
Folgende Tabelle zeigt den Stichprobenumfang, das relative Risiko, die Wirksamkeit und das Konfidenzintervall von Impfstoffstudien der vier Pharmakonzerne.
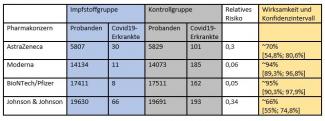
Konkret heißt das für das Beispiel des Impfstoffs von AstraZeneca: Die Wirksamkeit des Impfstoffs bei der Stichprobe in der klinischen Studie lag bei etwa 70%. In der gesamten Bevölkerung sollte sie aber zwischen etwa 55% und 81% liegen. Es bleibt zu beachten, dass sich die in der Tabelle genannten Wirksamkeiten nur auf die Reduktion von Erkrankungen und nicht auf die Schwere der Erkrankungen oder gar Todesfälle bezieht, welche durch Impfungen natürlich auch zum Positiven beeinflusst werden. Hier hat man in Studien für den Impfstoff von Johnson & Johnson einen Schutz von 85% und für die Impfstoffe von AstraZeneca, BioNTech/Pfizer und Moderna jeweils einen 100%igen Schutz erhalten können!
Fazit
Statistische Methoden erlauben es einem also anhand von Stichproben Rückschlüsse auf die Gesamtbevölkerung zu ziehen, und das mit überschaubarem Aufwand. Entscheidend ist hierbei natürlich die Repräsentativität der Stichprobe, ohne die jedes Resultat seine Aussagekraft verliert. Die besten Statistiken können also nur so viel verraten wie die Stichproben hergeben. Benutzt man die Konzepte jedoch gewissenhaft und auf Basis von vertrauensvollen Daten, dann kann man guten Gewissens Rückschlüsse auf die Gesamtbevölkerung ziehen.
Autoren: Gina Reuland & Julien Meyer (Luxembourg Science Center)
Editor: Michèle Weber (FNR)
Foto: Luxembourg Science Center
Simulation: Gina Reuland & Julien Meyer mithilfe von GeoGebra







